基于fast-planner改进的算法(1)-ego_planner阅读笔记

论文笔记

发布日期: 2021-10-21

文章字数: 4k

阅读时长: 14 分

阅读次数:

对应文章：EGO-Planner: An ESDF-Free Gradient-Based Local Planner for Quadrotors | IEEE Journals & Magazine | IEEE Xplore

对应代码：GitHub - ZJU-FAST-Lab/ego-planner

摘要

通过确定物体与障碍物表面距离，得到惩罚函数中的碰撞项
轨迹优化器只提取当前轨迹撞到的障碍物的信息，降低算法复杂度
如果某段轨迹动力学不可行，则延长该段轨迹分配的时间
异性曲线拟合算法——在保持原有轨迹形状的情况下降低轨迹的阶数

一、介绍

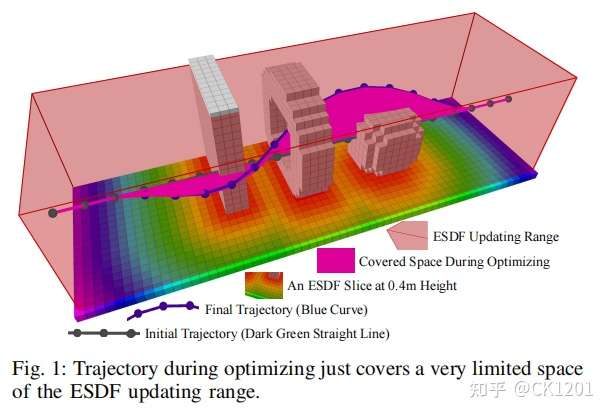
传统的基于梯度的运动规划算法需要构建所需的ESDF地图，然而构建地图花费了整个规划算法70%的时间，从而限制了在有限资源情况下的运动规划方法的使用。

ESDF的构建方式有全局增量式和批量本地计算两种方式，但他们并不是专门用于运动规划而构建的，也就是说对于运动规划来说现有的两种方法构建出的ESDF地图是多余的、不必要的。从图1中可以看出轨迹仅仅覆盖小范围的ESDF地图，大部分都是没用的。简单地手动减小ESDF地图范围，缺乏理论依据，也包含不必要的计算。

原文图1

EGO-Planer主要由基于梯度的样条曲线优化器和细化过程组成。

1.1基于梯度的样条曲线优化器

使用平滑性、碰撞性和动力学可行性项优化轨迹。碰撞项的构成通过比较障碍物内的轨迹与无碰撞的引导路径，然后用梯度信息将碰撞到障碍物的轨迹拉出障碍物，从而算法只需要计算碰撞处的障碍物梯度即可。

1.2细化过程

当某段轨迹动力学不可行时，激活细化过程，即增大该轨迹分配的时间。新生成的B样条曲线平衡了动力学可行性与拟合之前动力学不可行轨迹的准确性。在轴向和径向上拟合的准确性惩罚并不一样，以提高模型的鲁棒性。

二、相关工作

2.1基于梯度的运动规划

2.2带符号的欧式距离场（ESDF）

三、避撞力的估计

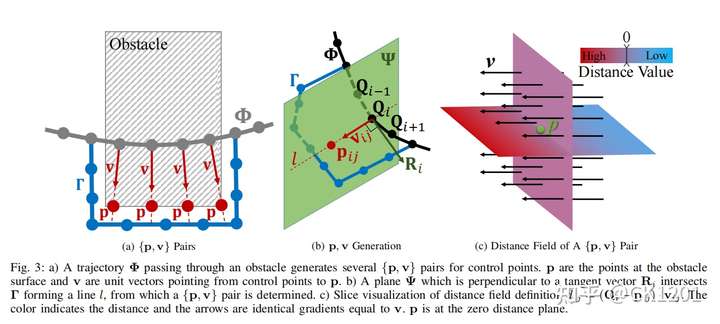
定义B样条曲线的控制点为Q，一开始生成一条满足终端约束但不考虑障碍物的B样条曲线 $\Phi$，接着，对于每段被检测到的碰撞的线段，用优化程序（这里使用的是A星算法）生成一个无碰撞的路径 $\Gamma$ 。对于发生碰撞的线段的每个控制点 ${Q_i}$ 都会生成一个在障碍物表面的定位点（anchor point） $p_{ij}$ ，且对应一个排斥单位方向向量 ${v_i}$与 ${Q_i}{p_{ij}}$同向(这里不应该是相等，${v_i}$为单位方向向量)。每对 {p,v} 对都对应一个特定的控制点Q。算法1为{p,v} 对的生成过程。

这里{p,v} 对的生成过程可以通过图3读懂，但是读到这里没懂没有关系，论文把大量关键点放到最后的实验内容才讲清楚。

原文图3

算法1伪代码：

优化算法1

算法1伪代码说明：

FindConsecutiveCollidingSegment(Q)找到与Q发生碰撞的障碍物，并判断其是否存在

GetCollisionSegment()提取出与Q发生碰撞的障碍物

.push_back()将障碍物添加入障碍物集合中

PathSearch()针对障碍物生成一个无碰撞的路径

Find_p_v_Pairs (Q,path)根据控制点与无碰撞路径确定匹配的{p,v}对

${Q_i}$ 到第 j个障碍物的距离如下，需要注意单位向量v在第一次生成后就不会再次发生改变，所以${d_{ij}} $的值是分正负的。

$d_{ij}=(Q_i-p_{ij})v_{ij} \tag{1} \\$

为了防止轨迹被拉出当前障碍物前，迭代过程中反复生成 {p,v} 对，判断是否为新障碍物的标准是：如果控制点${Q_i}$ 处于障碍物中时，并且对于当前得到的所有障碍物 j满足${d_{ij}} > 0$，则该障碍物为新发现的障碍物。从而只计算影响轨迹的障碍物信息，减少运行时间。

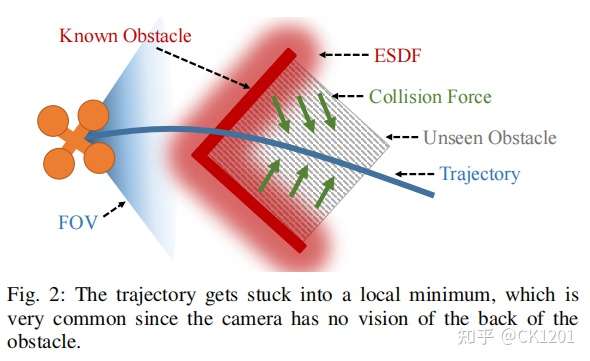
为了将必要的环境意识融入当地的规划中，我们需要明确地构建一个目标函数(设计基于梯度的轨迹优化器)，使轨道远离障碍。ESDF提供了这种至关重要的碰撞信息，但代价是沉重的计算负担。此外，如图2所示，由于ESDF反馈的错误信息不足，基于ESDF的规划者很容易陷入局部最小值，无法逃脱障碍。为了避免这种情况，额外的前端总是需要提供一个无碰撞的初始轨迹。由于明确设计的斥力对于不同的任务和环境都是相当有效的，所以上述方法在提供避免碰撞的重要信息方面优于ESDF。

原文图2

四、基于梯度的轨迹优化器

4.1问题建模

本文使用均匀B样条曲线 $\Phi$来表示轨迹（均匀B样条曲线可以参考B样条曲线绘制项目进行学习），其阶数为${p_b}$，均匀B样条曲线的每个节点有相同的时间间隔。

B样条曲线的凸包性质表明，某段曲线只与${p_b}+1$个连续的控制点有关，并且曲线被包含在这些点构成的凸包内。B样条曲线的k阶导数是 ${p_b}-k$ 阶B样条曲线。轨迹 $\Phi$ 的一阶、二阶、三阶导数的控制点分别为

$V_i=\frac{Q_{i+1}-Q_i}{\Delta t},A_i=\frac{V_{i+1}-V_i}{\Delta t}，J_i=\frac{A_{i+1}-A_i}{\Delta t} \tag{2}\\$

根据无人机的微分平坦特性降低要规划的变量，优化问题可以被定义为

$Q=argmin\ J=\lambda_sJ_s+\lambda_cJ_c+\lambda_dJ_d \tag{3}\\$

${J_s}$为光滑项惩罚， ${J_c}$为碰撞项惩罚，${J_d}$为动力学可行项惩罚， $\lambda $ 为惩罚项的权值。

4.1.1光滑项惩罚

在Real-Time Trajectory Replanning for MAVs using Uniform B-splines and 3D Circular Buffer (researchgate.net)中提出，光滑性惩罚被公式化为轨迹参数(加速度、加加速度等)的平方导数上的时间积分。由于B样条曲线的凸包性质，只要最小化轨迹 $\Phi$ 的二阶和三阶控制点的平方和就能够有效地减小加速度和加加速度的平方和。

$J_s=\sum_{i=1}^{N_c-2}\left|\left| A_i \right| \right|_2^2+\sum_{i=1}^{N_c-3}\left|\left| J_i \right| \right|_2^2 \tag{4}\\$

4.1.2碰撞项惩罚

碰撞惩罚使控制点远离障碍物，这是通过采用安全间隙和惩罚控制点${d_{ij}}< {s_f}$来实现的。为了进一步优化，我们构造了一个二次连续可微惩罚函数，并随着${d_{ij}}$的减小而抑制其斜率，从而得到分段函数

$j_c(i,j) = \begin{cases} 0, & c_{ij}\leq0 \\ c_{ij}^3, & 0\leq c_{ij}\leq s_f \\ 3s_fc_{ij}^2-3s_f^2c_{ij}+s_f^3,& c_{ij}>s_f \\ \end{cases}\\ \tag{5}$

$c_{ij}=s_f-d_{ij}$

对所有控制点的惩罚求和得到总的碰撞项惩罚

$J_c=\sum_{i=1}^{N_c}j_c(Q_i) \tag{6}\\$

相比于传统用三线性插值的方法求碰撞项的梯度，我们直接计算二次连续可微惩罚函数对${Q_i}$的导数来得到梯度：

$\frac{\partial{j_c}}{\partial{Q_i}} =\sum_{i=1}^{N_c}\sum_{j=1}^{N_p} \begin{cases} 0, & c_{ij}\leq0 \\ -3c_{ij}^2, & 0\leq c_{ij}\leq s_f \\ -6s_fc_{ij}+3s_f^2,& c_{ij}>s_f \\ \end{cases}\\ \tag{7}$

4.1.3可行项惩罚

通过限制轨迹在每一维上的高阶导数来保证其可行性。由于凸包的性质，对控制点的导数进行约束足以约束整个b样条。F()为为每个维度的高阶导数构造的惩罚函数。

$J_d=\sum_{i=1}^{N_c-1}\omega_vF(V_i)+\sum_{i=1}^{N_c-2}\omega_aF(A_i)+\sum_{i=1}^{N_c-3}\omega_jF(J_i)\tag{8} \\$

$F(C)=\sum_{r=x,y,z}f(c_r)\tag{9}\\$

$f(c_r)=\begin{cases} a_1c_r^2+b_1c_r+c_1, & c_r<-c_j \\ (-\lambda c_m-c_r)^3, & -c_j < c_r < -\lambda c_m \\ 0,& -\lambda c_m \leq c_r \leq \lambda c_m \\ (c_r-\lambda c_m)^3, & \lambda c_m < c_r < c_j \\ a_2c_r^2+b_2c_r+c_2,& c_r>c_j \\ \end{cases}\\ \tag{10}$

可以看出问题建模中应用的惩罚函数全部是多项式和，这有利于降低求解最优化问题的复杂度。（轻量化算法）

4.2最优化求解方法

目标函数 J会随着新障碍物的加入而不断改变，这就要求求解器能够快速重启，并且目标函数主要由二次项组成，所以Hessian（黑塞矩阵）信息能够加快收敛速度。但得到精确的Hessian消耗大量计算机资源。所以我们使用拟牛顿法（ quasi-Newton methods)从梯度信息中来近似计算Hessian。

在对比了Barzilai-Borwein method、truncated Newton method和L-BFGS methodh后发现，L-BFGS表现最好，平衡了重启损失和逆Hessian估计的准确性。L-BFGS从以前的目标函数评估近似Hessian，但需要一系列的迭代，以达到一个相对准确的估计。

上述几种最优化求解方法在我们的最优化课本中就有提及

五、时间重分配和轨迹细化

基于四节中得到的安全轨迹生成一条时间分配合理的均匀B样条曲线轨迹 ${\Phi_s}$ ，然后使用各向异性曲线拟合方法（an anisotropic curve fifitting method）使 ${\Phi_f}$ 自由地优化其控制点，以满足高阶导数约束，同时保持与 ${\Phi_s}$几乎相同的导数形状。

首先计算超过限制(下标m表示限制的最大值)的比例,

$r_e=max\{ \left| V_{i,r}/v_m \right|,\sqrt{\left| A_{j,r}/a_m \right|},\sqrt[3]{\left| J_{k,r}/j_m \right|},1 \}\tag{14}$

${r_s}$ 表明相对于 ${\Phi_s}$ ， ${\Phi_f}$ 需要分配多少时间。 ${V_i}$ ， ${A_j}$ 和 ${J_k}$ 分别与 ${\triangle{t}}$ 的一次、二次和三次成反比，通过与时间的反比关系可以降低速度及其导数，则 ${\Phi_f}$ 的新时间间隔为

$\Delta t'=r_e\Delta t \tag{15}$

通过求解一个如下的闭式的最小二乘问题，在速度及其导数的约束下初始生成时间跨度为${\triangle{t}^{\prime}}$ 的轨迹${\Phi_f}$ ，同时保持与 ${\Phi_s}$ 相同的形状和控制点数。然后重新计算光滑项惩罚和可行性项惩罚得到新的目标函数

$Q=argmin\ J’=\lambda_sJ_s+\lambda_dJ_d+\lambda_fJ_f \tag{16}$

${J_f}$ 被定义为从 ${{\Phi_f}(\alpha T^{\prime})}$ 到 ${{\Phi_s}(\alpha T)}$各向异性位移的积分，其中 $T$ 和 $T^{\prime}$ 为轨迹 ${\Phi_s}$ 和 ${\Phi_f}$ 的时长，其中$\alpha \in \left[ {0,1} \right]$。

由于拟合的对象曲线 ${\Phi_s}$ 已经无碰撞，对于两条曲线，我们用带有低权重的轴向位移 ${d_a}$ 来放宽光滑调整限制，用高权重的径向位移 ${d_r}$ 来防止碰撞。如图5所示，我们使用球状度量来使在同一球体表面的位移产生相同的惩罚。(关于径向位移和轴向位移应该在具体算法中了解，目前我认为轴向位移为该点的切线方向，而径向方向为该切线的垂线方向)

原文图5

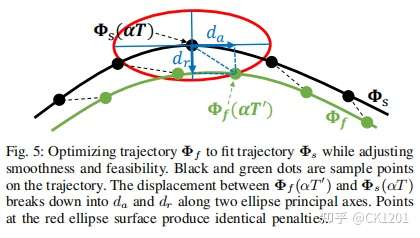
用于度量 ${{\Phi_f}(\alpha T^{\prime})}$ 惩罚大小的椭圆体是一个以 ${{\Phi_f}(\alpha T^{\prime})}$ 为中心的椭圆，其半长轴长度为a、其半短轴长度为b。则轴向位移 ${d_a}$ 和径向位移 ${d_r}$ 为

$d_a(\alpha T')=(\Phi_f(\alpha T')-\Phi_s(\alpha T))\cdot \frac{\dot{\Phi_s}(\alpha T)}{\left| \left| \dot{\Phi_s}(\alpha T) \right| \right|}\\ d_r(\alpha T')=\left| \left| (\Phi_f(\alpha T')-\Phi_s(\alpha T))\times \frac{\dot{\Phi_s}(\alpha T)}{\left| \left| \dot{\Phi_s}(\alpha T) \right| \right|} \right| \right| \tag{17}$

则拟合惩罚项可表示为为 $J_f=\int_{0}^{1}\left[ \frac{d_a(\alpha T')^2}{a^2}+\frac{d_r(\alpha T')^2}{b^2} \right]d\alpha \tag{18}$

其中a和b分别是椭圆的半长轴和半短轴，径向位移对应的半短轴b使径向位移的惩罚权重增大以防止防止碰撞。

式18被离散化为有限个数的点 ${\Phi _f}(\alpha \Delta {t^\prime })$ 和 ${\Phi _s}(\alpha \Delta t)$ ，其中

$k \in \mathbb{R}$

$0 \leq k \leq \lfloor T/\Delta t \rfloor$

六、实验结果

6.1实验细节

规划算法框架如算法2所示。

算法2

算法2伪代码说明

FindInit(Q,G)生成一条满足终端约束但不考虑障碍物的B样条曲线 $\Phi$对应的控制点

IsCollisionFree(E，Q)判断控制点是否在环境中是无碰撞的，有碰撞时输出false

CheckAndAddObstacleInfo(E,Q)检测控制点所在障碍物，并添加障碍物信息({p,v}对以及距离场)

EvaluatePenalty(Q)根据问题建模构造控制点相应惩罚项J以及对应的梯度

OneStepOptimize(J,G)求解惩罚项的最小化问题，即最优化求解，从而得到满足惩罚项的最小化的控制点位置，即完成第一步的轨迹优化

IsFeasible(Q)判断由控制点Q决定的轨迹是否可行(主要是速度以及其多阶导数否超过限制最大值)

ReAllocateTime(Q)通过重新分配由控制点Q决定的轨迹的时间降低速度以及其多阶导数，使其满足各类速度约束。

CurveFittingOptimize(Q)将之前的惩罚中碰撞项替换为曲线拟合项，求解惩罚项最优化问题。使其在满足新时间间隔的前提下，拟合由旧控制点构成的轨迹得到新轨迹，在继承旧轨迹的无碰撞特性的前提下实现约束下可行性。

我们设置B样条曲线的阶数${p_b} = 3$，控制点的个数 ${N_c}$ 为25左右，具体由规划预期距离（大约7m）和初始的邻近点间距（大约0.3m）决定。这些参数根据经验通过平衡了问题的复杂度和自由度而得到。

因为根据B样条曲线的性质，一个控制点只影响周围的轨迹，所以算法的时间复杂度为 $O({N_c})$。

L-BFGS的复杂性在相同的相对公差上也是线性的。(The complexity of L-BFGS is also linear on the same relative tolerance)

在无碰撞路径搜索中，我们采用A星算法进行轨迹优化，而它生成的轨迹$\Gamma $常常贴着障碍物。因此，我们可以直接在A星算法生成的轨迹$\Gamma $上选择定位点（anchor point）p 而不用搜索障碍物的表面(这里才真正解释出了第三节中A星算法的作用)。对于图3b中定义的向量$R_i $，通过均匀b样条参数化的性质，可以推导出

$R_i=\frac{Q_{i+1}-Q_{i-1}}{2\triangle t} \tag{19}$

这里的$R_i$是图3中确定{p,v}对的关键。

读到这里，我们再看看论文中的图3。

第一步：根据生成一条满足终端约束但不考虑障碍物的B样条曲线 $\Phi$，依靠A星算法生成的轨迹$\Gamma $。

第二步：根据公式(19)通过B样条曲线的控制点计算出向量$R_i $，再做出垂直于$R_i $的平面$\Psi $，平面$\Psi $与依靠A星算法生成的轨迹$\Gamma $相交于定位点（anchor point）p，连接对应的定位点（anchor point）p与控制点Q，才得到直线l,而向量v是向量l对应的由起点控制点Q到终点定位点p对应的单位向量。(v可能是生成以后不会再变化的)。到这里才生成了{p,v}对。

论文第3节的内容到第6节才彻底解释清楚，真是折磨死我了！！！

note：思考问题：关于{p,v}对过程中，为什么将定位点p定位到A星算法生成的贴着障碍物的轨迹上，而不直接定位在障碍物表面？

我的理解：在A星算法生成的轨迹(线)定位的算力成本比直接定位在障碍物表面(面)低。

原文图3

为了进一步保证安全，对最终轨迹周围具有固定半径的圆形管道进行碰撞检查，以保证轨迹和障碍物之间有足够的距离，优化程序在未检测到碰撞时停止。

真实世界的实验环境与Teach-Repeat-Replan相同，此外，我们还修改了Intel RealSense的ROS驱动程序，使激光发射器每隔一帧频闪。这使得该设备在发射器的帮助下输出高质量的深度图像，以及不受激光干扰的双目图像。修改后的驱动也是开源的。

6.2优化算法的比较

6.3有/无ESDF的轨迹生成

6.4多个规划器的比较

6.5真实世界实验

七、结论和未来的工作

该方法仍然存在一些缺陷，即A*搜索引入的局部最小值和统一时间重新分配引入的保守轨迹。因此，我们将致力于执行拓扑规划，以逃避局部最小值，并重新制定问题，以生成接近最优的轨迹。规划器为静态环境设计，无需处理缓慢移动的障碍物（低于0.5m/s）。在未来，我们将通过移动对象检测和拓扑规划来研究动态环境导航。

以上内容根据博客：EGO-Planner论文阅读笔记 - 知乎 (zhihu.com)进行补充与修改。